Purpose of the model
The model is designed to realistically simulate typical week-day passenger journeys in Canberra in the year 2022, and to estimate the costs of providing an on-demand, 24x7 autonomous car service to provide those journeys.
The default model assumes the specifications of a currently-available electric vehicle (Tesla 3 Standard Range+, November 2020 "Made in China" build). It further assumes this vehicle will, by 2025, have a "true" Full Self Drive option, allowing them to be fully autonomous. It is this assumption which is currently (as at the end of 2022) speculative: whilst there are many promising developments and trial systems, no-one has yet delivered a general, commercial, widely available autonomous vehicle (more below). All other settings of the default model detail below are conservative: that is, if, for example, Tesla, Waymo or others succeed in widespread deployment of autonomous driving by 2025, then this model probably accurately simulates the characteristics of a fleet of autonomous vehicles providing the vast majority of passenger journeys around Canberra.
The simulation aims to be useful by being flexible and fast at the expense of being completely comprehensive and optimised. It is designed to be conveniently runnable (in a web browser) for high usage scenario on common hardware, taking just a minute or two elapsed, and to present the results in a way to facilitate their interpretation, comparison and sanity-checking.
Although the financial aspects of the ongoing operation of an autonomous vehicle fleet is modelled, the "start-up" and "ramp-up" phases are not modelled.
Overview of model
Before running each simulation, the model generates an estimate of the number of arrivals and departures using the current parameters for each suburb for each minute as follows:
- It first generates an estimate for the number of trips which will depart in any one minute, based on the total number of journeys and their per-hour distribution as specified to the model.
- For each minute, this total number of departing journeys is randomly "dithered" to be within a -20% : +20% range, with a simple linear probability gradient up from 0 at the lower (-20%) bound, rising to the centre of the range and then back down to 0 at the upper (+20%) bound. This does not produce a normal distribution, but instead imagine 2 right-angled triangles back to back. This total number of departing journeys is then distributed randomly to each suburb based on the probability of each suburb being a journey source for the minute of the day under consideration [more...]. The destination suburb is then randomly chosen based on the probability of each suburb being a journey destination for that minute, with bias resulting in nearby suburbs are slightly more probable destinations. (The local-travel bias depends on where the suburb is - this so-called "self-containment" information used in this model was derived from findings of ACT and Queanbeyan-Palerang Household Travel Survey based on travel patterns over October and November 2017.)
- The above estimation is run twice (representing 2 "days"), and the average values of arrivals and departures per minute for each suburb are passed to the "real" simulation for it to use as its best estimate to predict the demand for and supply of cars it will see when it runs over its "day" to forecast demand for each suburb and this forecast demand is used to pre-emptively transfer cars to meet forecast demand.
The "real" simulation then runs, independently generating a dithered total journey demand rate for each minute and completely independently assigning source and destination suburbs for each journey.
This dithering means that the "real" simulation demand for cars from each suburb and arrival of cars at each suburb will vary considerably from the forecast it is provided, tending to reduce the effectiveness of demand forecasting and pre-emptive transfer of cars, as would happen in the real world: in the "real world", much better forecasts of demand would be available both from history and from imminent bookings ("I'd like a car here in 3 minutes"), and hence the more random demand in this simulation tends towards a "worst case" scenario.
Major limitations of the model
Discrete rather than continuous time
No specific addresses
Inter-suburb travel times, routes and distances are estimated from OpenStreetMap and GraphHopper services
All journey requests are for immediate travel
Simple sharing
Poor or no fleet optimisation
- Once charging begins, a car is always charged to 80%. Often, a car charged to, say, 65% should be reassigned to service waiting passengers rather than continue charging to 80%.
- Forward load anticipation is naiive, being based solely on the anticipated difference between supply and demand of cars at each suburb in 15 minutes. Decisions to transfer cars between suburbs are mostly based on this simple measure.
- Car transfer is naiive. For example, imagine location A is 10km north of location B which is 10km north of location C and that a 10km journey takes 15 minutes. Based on forecast demand, A has 10 spare cars, B has 1 spare car, C is short of 1 car. The system will currently transfer a car from A to C, which will take 15 minutes longer than necessary: a better strategy is to simultaneously send a car from B to C and from A to backfill the car sent from B - same total distance, but C's need is satisfied 15 minutes sooner.
Charging time of day
It is possible that an operational system will have constraints on power consumption, for example, during the morning and evening household electricity usage peaks. Alternatively, there may be strong incentives to use power during solar-PV peak outputs.
Such constraints could influence choices such as car battery capacity, charging rates, number of chargers and even number of cars.
The current model reduces charging during the evening home-power-use peak between 6pm and 9:30pm.
Single vehicle type
This model treats each vehicle as interchangeable and does not support vehicles of mixed specification (particularly range and seating capacity). It is not clear whether having a mix of vehicles with different specifications would be beneficial.
Weekend (non-weekday) outcomes are estimated, not simulated
Non-weekday travel patterns are very different, and are not simulated. Rather, the financial outcome for these days is estimated using a heuristic described below.
Financial incentives associated with car sharing
Perhaps unrelated passengers sharing a car due to a system scheduling decision should receive a discount. Perhaps guaranteed unshared peak period use of a car regardless of route should be available for an extra fee.
Major known unknowns
Commercial availability of autonomous cars
As at November 2020, there is only one commercially operated fleet on autonomous vehicles (Waymo) and its fully autonomous (no safety driver) range is limited to eastern Phoenix. Tesla, Ford/Argo, Baidu, GM/Cruise and others have announced commercial fully-autonomous capabilities starting in 2021, 2022 or shortly thereafter, and there are many convincing arguments and expert opinions predicting their availability in time-frames ranging from 2021 to 2028. However the date of the commercial availability of a fully autonomous car is the biggest unknown and risk.
Specifications and cost of a suitable autonomous electric vehicle
The range of electric vehicles are improving and their costs are reducing. Whilst this model suggests that the viability of a transport system based on autonomous EVs is not particularly sensitive to range, it is extremely sensitive to capital costs and per-km running costs.
The default vehicle specification and cost used in this simulation is the November 2020 version of Tesla Model 3 Standard Range Plus, with the FSD (Full Self Driving) option. This default settings in this simulation assume the vehicle has a 'real world' range of 410km and a usable battery capacity of 55kWH, and uses about 135wH/km when travelling, to which 5wH/km is added to cover power use when not moving (for the default simulation parameters, this adds a further consumption of 1.8kW/day).
Although these specifications are likely to have slightly improved by 2025, these current values are assumed by the default model.
Cost are harder to assess (details below).
Battery degradation
With the default model assumptions for vehicle type, fleet size and service levels, the simulation suggests that over a 3 year period, each vehicle will travel about 375,000km. The simulation aims to never charge batteries above 80%, and trigger recharges when capacity falls to ~25%. (In a typical simulation run, less than 3% of cars fall to under 15% of charge before being charged and less than 0.05% fall to under 10% of charge.) Conventional wisdom suggests avoiding both high and low battery charge states tends to prolong battery life. Over 3 years of the default simulation settings, the equivalent of just under 900 "full" cycles (although no full cycles will ever be performed due to the 20%-80% charging range).
In April 2019, Elon Musk claimed that the Tesla Model 3 drive train and body was designed for a "million mile" life, and the current batteries for "300k - 500k miles (1500 cycles)" (ie, 480k - 800k km). The default model parameters should result in insignificant battery degradation over the 3 years service life, and indeed, assuming a mid-point of ~640,000 km battery life, vehicles will have a typical post-fleet life of 265,000 km using the original batteries. More below..
Location of charging stations
The default model assumes 1200 chargers distributed over 9 locations to minimise travel times/distances required for recharging. It probably makes sense for some or all of these locations to also contain maintenance (including workshops and spares stored), cleaning and some admin facilities (and the model assumes cars can undergo quick-cleans whilst they are being charged). Some charging stations could reuse some freed space and infrastructure such as government car parks and bus depots. It may be optimal to use more than 9 charging stations (with fewer chargers in each) to minimise travel for recharging and traffic at chargers.
Access to a high-capacity power supply is required. With the default model parameters, the largest charging station at Belconnen would house over 230 chargers and consume about 35MW.
Autonomous charging
The default model results in around 75,000 recharges each day. Requiring human intervention to connect and disconnect a charging cable would be expensive and inefficient. However, although touted in 2015, automatic charging for electric vehicles is not commercially available (although it may be in a few years). Hence the default model does not assume automatic charging, but that the cost for manual connection and disconnection of the charging cable forms part of the "per km" cost valued at 0.8 cents/km. [The default model results in a charge event every ~175km of travel. Assuming connecting and disconnecting cable requires a total of 2 minutes of labour (as part of a 6 minute total labour per visit to the charging station), at an effective labour cost of $39/hour, charger costs $1.30 in labour, or 0.8 cents/km.]
Actual travel patterns in Canberra, now and in 2022
The model uses heuristics to randomly generate a different set of journeys each time it is run, based on travel statistics reported by the ACT and Queanbeyan-Palerang Household Travel Survey. The outcomes of the model are not particularly sensitive to travel patterns except for two which are always faithfully reproduced:
- The narrow and steep AM and to a lesser extent, PM peak demand, which fundamentally determine fleet size for any given upper-cap on waiting times. That is, the fleet is "sized" to meet waiting time objectives set for the AM peak.
- Peak-period flows are "tidal": towards the employment centres in the AM peak, and towards the suburbs in the PM peak.
Different travel patterns may emerge with increased working and shopping from home, or with the availability of an inexpensive, on-demand, door-to-door, 24x7 autonomous car service.
Administrative and operational costs and system requirements
The default model includes a fixed annual $15M cost for admin and general system running costs (general management, customer service, web-site, fleet scheduling, billing, lost-property...) plus separate fixed annual provisions of $4000 per car consisting of:
- $1000 for third party insurance
- $350 for customer liability insurance
- $150 for workers compensation insurance
- $1000 for registration and other road-user fees
- $50 for mobile communications
- $500 for workshop/maintenance fixed costs
- $450 for other than "per-km" labour costs, such as acquisition, commissioning, decommissioning, and warranty management
- $500 for other than "per-km" parts and consumables costs not covered by warranty, for example wear-and-tear, vandalism or accidental damage
The capital and financing costs of each car also include the cost of a fleet of 5% of "spare" cars.
A separate cost default "running" cost of 5c/km (details below) includes the variable costs attributable to car usage (cleaning, maintenance etc). Power costs are also calculated separately.
Congestion
This model does not attempt to measure congestion. Travel-times are based on estimates from OpenStreeMap and GraphHopper, increased by 15% for peak periods as described here. However, it would be interesting to monitor route loadings to determine peak vehicles per lane km and intersection crossings.
It is not obvious what levels of autonomous traffic can be tolerated. Simulations using the University of Texas at Austin's Autonomous Intersection Management project suggest "intelligent" intersections can coordinate vehicle approaches and traversals to handle three times the throughput of an intersection controlled by traffic signals. (See also the DriveWAVE intelligent intersection work from the MIT Senseable City Lab.) An analysis of coordination and "platooning" of autonomous vehicles suggests they could increase lane capacities by a factor of three.
This is not to say that congestion analysis is unwarranted, particularly when considering a mixture of autonomous and non-autonomous vehicle flows, but traditional measures of road and intersection capacity and congestion may need modification.
The simulation does provide some results suggesting that congestion in peak periods will be lower the higher the uptake, despite "dead running" needed to transfer cars in periods of "tidal" flows. For example, consider the results from the "Default 2022" journey simulation's "Occupancy data" section. It shows high average occupancy of cars arriving in AM peak at commuter "sinks" - work centres such as Civic, Parkes, Barton, Russell, and the ANU. It also shows the occupancy of cars leaving Gungahlin, Belconnen and Tuggeranong in the AM peak, regardless of the destination.
With "tidal" flows, a shared fleet of autonomous cars increases the volume of cars going "against" the flow, as empty cars need to reposition from the commuter "sink" to the commuter "source" to pick-up more passengers. But, by definition, these repositioning cars are travelling on otherwise under-utilised roads (few people want to be going in that direction, which is why the repositioning cars are empty).
Configurable model parameters
Cars
Fleet size - number of cars on the road
Purchase cost
The default cost is $65,000, excluding GST and acquisition costs.
The (January 2021) cost in $A of a Tesla Model 3 SR+ with Full Self Driving (FSD) manufactured in the USA and including delivery within the USA is $A62,380. Assuming Model 3's manufactured in China are slightly cheaper to manufacture (labour, newer lithium-iron-phosphate batteries) and to ship to Australia, and also assuming a continuation of a slight decline in prices compared to specifications over the next few years, but adding the cost of shipping from China to Canberra, the default simulation assumes a fleet purchase per-vehicle price of $A65,000. GST is not included as a net cost: this simulation assumes that either the fleet owner is the ACT Government (and any GST paid will be repaid as a GST distribution from the Commonwealth, and hence does not represent a net cost to the ACT), or for a private fleet owner, GST input tax is exceeded by GST on fare collection (hence does not represent a net cost to the fleet owner).
Residual Value
Using the default simulation parameters, cars can be expected to have travelled around 375,000 km over 3 years, and undergone around 900 full battery cycles (albeit mostly confined to the 20%-80% charging range).
This usage is significantly less than the design life claimed by Tesla for the Model 3: drive train and body - "a million miles", battery for ~640,000 km (midpoint of their claim) and 1500 cycles.
Hence vehicles will have a remaining (post-fleet) battery life of around 265,000 km and will have the Full Self Driving (FSD) option, currently (Nov 2020) selling in the USA for the equivalent of $A14,200, a value included in the purchase cost calculation above.
Some cars will be written off, but the fleet includes 5% "spares" which the model assumes will cover these loses and supply parts for some vehicles.
The model assumes financing of the fleet as follows, given an initial purchase cost of each car of $P, an average disposal value of each car of $D, a financing (or leasing) period of Y years and an annual interest rate of I% :
- capital of ($P - $D) to be repaid over Y * 12 equal monthly payments
- interest to be paid monthly on outstanding (unrepaid) capital, with interest payments averaged over the loan period: ($P + $D) / 2 * (I% / 12)
For example, for a purchase price of $65,000, and average residual value of $14,000, a 36 month life and 4% interest rate, then for each car (including the spares):
- Monthly capital repayments are: (65,000 - 14,000) / 36 = $1,417
- Monthly interest payments are (65,000 + 14,000) / 2 * 4% / 12 = $132
The default model's average residual value of $14,000 is estimated as follows:
- 5% of the fleet will have zero residual value - these are cars totally written off or cannibalised for spare parts
- 60% of the fleet will be in good condition, no damage to interior or exterior bodywork, will have 250,000+km of battery lifetime remaining and a FSD license, and will have a residual value of $20,000 (ie, $5,000 more than the value of the FSD license).
- 25% of the fleet will be in fair condition, minor interior or exterior damage, will have over 100,000km of battery lifetime remaining and a FSD license and will have a residual value of $10,000 reflecting the cost of minor repairs and battery module replacement necessary to bring them up to good condition.
- 10% of the fleet will be in poor condition with more extensive interior or exterior damage, will have less than 100,000km of battery lifetime remaining and a FSD license and will have a residual value of $2,000 reflecting the cost of more extensive repairs and battery module replacement necessary to bring them up to good condition.
Useful Life
The default is 36 months.
A longer life reduces capital costs but should be accompanied by an increase in per-km maintenance costs and perhaps size of the spares.
According to the New York City Taxicab Fact Book, the average NY cab is 3.3 years old (so its life would be considerably longer, but must not exceed 6 years by law) and drives 70,000 miles (112,700 km) each year.
Financing interest rate
The default is 4%.
As of Nov 2020, Westpac's 5 year (fixed) business loan rate is 3.65% and their 3 year fixed rate is 2.79%. The yield on a 10 year Australian Government bond is just under 1% and the coupon on NSW TCorp Domestic State Guaranteed Bonds maturing in 2031 is 2%.
In the interest rate environment of 2020, Government and even commercial borrowing costs of 4% are very pessimistic.
Per-km travelled maintenance costs
Cleaning and charging labour costs are based on a wage rate averaged over all shifts of $32/hour plus a 20% overhead for non-productive time (but paid, giving a labour cost of $40/hr) for breaks, meetings, training and a 10% management overhead, giving a gross cost of $44/hour.
The default model per-km maintenance cost of 6.0c/km (equivalent to an annual per car cost of about $7735/yr) is estimated as follows:
- Per-charging-visit charger connection and disconnection and clean: 2.65 cents/km.
(~$3420 per car/yr)
With the default model parameters, on average each car visits a charger 2.1 times each day after travelling 175km between charges. The time to attach and detach the charger is estimated at 2 minutes, and the "per-visit" clean is estimated at 3 minutes, and the estimated idle time between cars is estimated at 1 minute, for a total labour time of 6 minutes and cost of $4.40. Assuming consumables of 25 cents per clean gives a total cost of $4.65 rounded to 2.65c/km.
- Weekly clean: 0.5 cents/km (~$640 per car/yr)
Assuming a 15 minute thorough clean costing $11 in labour and $0.50 in consumables every week, or approximately 2400km travelled, the per km cost is rounded up to 0.5 cents per km.
- Tyres, general maintenance and repairs: 1.75 cents/km (~$2225 per car/yr)
The default model includes a separate cost for the purchase of complete spare cars, sized at 5% of the fleet. That is, for the default model fleet size of 34,000 cars, 1,700 extra cars are purchased as spares and for spare parts, and the cost and financing of these spares is included in the per-car capital and financing costs, not this "per-km" component. In addition, the fleet will be covered by the manufacturers warranty for its first of three years (although tyres are not included).
A 2019 analysis of the 5 year cost of ownership of a Tesla 3 estimated repairs and servicing/maintenance cost of $US1200 ($A1700) over 5 years and 108,400km of travel, equivalent to 1.6 Australian cents per km.
- Other maintenance/repairs not covered by warranty and/or spare parts from fleet "spares": 1.15 cents/km. ($~1450 per car/yr)
Absent from these maintenance costs are explicit allowances for:
- Most accident repairs. The liability for most of these costs will rest with the human driver crashing into the autonomous vehicle, or the manufacturer of the autonomous system that failed. However, the annual non per-km costs includes
- Faults covered by warranty (such as breaking door-handles and electric windows, cars catching fire). The vehicles will be less than 3 years old, and a manufacturer's warranty is assumed to be negotiable as part of the large fleet purchase, plus the extra (by default) 5% of the fleet size purchased as "spares". At a 5% ratio of spares, 1 in 60 cars can be assumed to be "written off" each year.
- Battery replacement. Hitherto, the biggest uncertainty regarding EV maintenance costs has been battery replacement due to degradation resulting from both calendar age and cycles. However, as mentioned above, Tesla are claiming a battery life that significantly exceeds the distance travelled and cycles modeled in this simulation.
The summary breakdown of the 6.0c/km default model cost to labour and parts is:
- labour: 4.3c/km
- tyres: 0.8c/km
- other parts and consumables: 0.9c/km
Annual non per-km costs: insurance/rego/fleet management/contingencies
The default model cost is $4000, estimated as follows:
Insurance: $1000 for compulsory third party insurance and third-party property damage.
It is hard to estimate insurance costs, as one of the primary advantages posited for autonomous cars is the reliability of the "driver" who is never tired, distracted by passengers or their phone, fiddling with their radio, drunk, incapacitated nor overcome by road-rage.
The "spares purchased" part of the fleet provides some self-insurance for repairs and write-offs.
A government-run fleet would probably "self insure".
Customer liability insurance: $350
(That's an allocation of about 3.5c per passenger trip)
Workers compensation insurance: $150
(For the default simulation, that's an allocation of just over 2.5% of all wages and superannuation payments, which is a typical premium level for the transport sector)
Registration and road-use fees: $1000
Mobile communications: $50
Cars may send a 4K of TCP data to report their status every 5 seconds, and another 100K for events such as pick-ups and set-downs. Bulk data (video? software updates?) can be transferred using wifi during charging. So, daily mobile data requirements may be 24*60*12 4K status packets plus ~80 100K event packets = max 100MB/day. Assuming a commercial plan charging $1/GB, that's max $50/year.
Workshop/maintenance fixed costs: $500
For per-car fixed costs related to workshop and maintenance space and staff facilities
Non "per-km" labour costs: $450
For acquisition, commissioning, decommissioning, and warranty management.
Non "per-km" parts and consumables costs: $500
For consumables and parts not covered by warranty, for example wear-and-tear, vandalism or accidental damage.
Real-world Maximum Range
The default is 410km, based on the Tesla Model 3 SR+ "made in China" (55 kWh using LFP batteries) November 2020 NEDC range of 468km reduced by 10% to better approximate "real world" conditions (including use of heating and cooling and power use whilst idle) then rounded down a few more percent to 410km.
Given the consistent range improvements EVs and in particular, Tesla, have delivered over the past few years, as a maximum range is probably conservative for 2022.
Energy usage per km
Passenger capacity
The default is 4.
The Tesla Model 3 transports 5 adults, but it is assumed paying passengers would rather wait a minute or two for an empty car than be stuck in the middle of the "back" seat.
The current model tries to share cars between passengers starting from the same suburb and travelling to the same suburb or a destination that requires only a small extra travelling time for any passengers. For simulations with low numbers of journeys, car sharing is rarely possible because the likelihood of passengers being able to share cars is low. For the "high" journey models, car sharing is only used in peak hours. Outside peak periods, a journey request is always effectively booking a "car", not a seat.
That is, a family of 4 (or 5) going to the movies, or 2 friends going home together after dinner, or a single person going to start their late shift all pay the same rates. During peak periods, many trips will be shared, but perhaps a premium could be paid by passengers who did not want to share, or wanted to book a car not a seat (for example, when travelling with their children). However, many peak-period trips are not candidates for sharing. For example, the fleet management system is keen to return an excess of cars accumulating at town centres back to suburbs during the morning peak period: at such times, trips from town centres to suburbs can be booked without sharing. Similarly, most suburb-to-suburb trips will not be shared.
What about large families, with say, more than 3 children, or a large group of people travelling together? As is required now with current sedans and taxis, more than 1 car will be needed. At least most of the time (and all of the time "off peak", including week-ends), only one fare needs to be paid per car per booking, so a family of, say 7 people booking 2 cars would almost always only pay 2 fares. For some families, being separated into 2 cars will be unacceptable and they will keep their Tarago. The NSW Bureau of Transport Statistics 2011/12 Household Travel Survey measured just 1% of weekday trips and 3% of weekend trips where the vehicle occupancy was 5 or more (Table 4.8.4). Unfortunately, the vital "6 or more" figure is not available from this report.
Spares purchased
The default is 5%.
It is assumed that the on-road fleet is sized to just meet peak capacity. However, cars will be off the road for maintenance, or will be written-off in some circumstances. Hence a pool of "spares" is required as replacements, but note, not as a contingency for a load spike, as this would require them to be also insured and registered, which is not costed in this model.
These spares could also be considered as a source of spare-parts: panels, windows, motors, etc, and hence prepay the costs of these and guarantee their availability. A 5% spare capacity represents a capacity to provide 1 complete spare car per year for every 60 cars on the road.
Charging
Number of chargers
Charge power (averaged over the entire charge)
The model default is 120kW, and assumes the purchase of 150kW chargers which will deliver an average 120kW to the maximum charge capacity of 80%.
Purchase cost
The model default is $70,000.
This estimate is based on anticipated commercial prices for very large purchases of 150kW+ DC EV chargers (not requiring "retail" capabilities) in 2022 (~A$45,000) and estimated installation costs of ~$A25,000 per charger from Table 4 of Estimating electric vehicle charging infrastructure costs across major U.S. metropolitan areas by Michael Nicholas, published by The International Council on Clean Transportation in 2019.
Useful Life
The default is 120 (10 years).
Annual Costs
The default is $2000 (ie, $2M pa for 1200 chargers)
Cost of electricity per kWh
Power usage in the default model would make it the largest electricity consumer in the ACT. The ACT Government announced an off-take agreement with Neoen for 100MW at $0.045/kWh, fixed for 14 years, so the default of $0.12 is probably quite conservative. See Electricity Price Update November 2025 (below) for more details.
Operating surplus is quite sensitive to the price of energy.
Journeys
Journeys per day
This survey estimated 1.2m person-trips undertaken within the travel area by car (as driver or as passenger) or by public transport. The default journey load for this simulation assumes 0.1m of those journeys could not be replaced by a journey in a shared fleet of autonomous vehicles: they will be transporting a person with specialised tools (eg, a plumber) or transporting bulky goods. As well, some of those journeys are of drivers whose only purpose is to deliver a service to a passenger, and would often not be required were a fleet of autonomous vehicles available.
Per hour distribution
The default is taken from the same report, ACT and Queanbeyan-Palerang Household Travel Survey conducted in late 2017.
Interesting alternatives include Estimating urban traffic and congestion cost trends for Australian cities, Bureau of Transport and Regional Economics Working Paper No 71 Figure 2.23 page 84, Network (arterial) average, VicRoads Traffic Monitor 2012-13, September 2014 page 15, "Monitored Network Traffic Profile" (although the right-hand scale seems a bit strange with uneven increments), and NSW Bureau of Transport Statistics 2011/12 Household Travel Survey Fig 3.9.1 (note: travellers, not vehicles).
The model distributes traffic volumes with a "tidal" bias over the day:
- 04:00 - 9:59: from suburbs to centres
- 10:00 - 14:59: no bias
- 15:00 - 18:59: from centres to suburbs
- 19:00 - 20:59: from suburbs to centres
- 21:00 - 03:59: from centres to suburbs
The propensity for a suburb to be a journey source and destination depends on the suburb definition in the TownAndSuburbs.js file (parameters which for each suburb define population and factors which define the factors: peakSource, peakDest, dayOffPeakSource, dayOffPeakDest, nightOffPeakSource, nightOffPeakDest.
The alternative model presents an alternative distribution with a "flatter" curve which greatly reduces the fleet size needed to service the peaks.
Fares
Peak flag fall
The default is $0.40
The logic behind having a flag fall is that the system incurs a real and fixed cost to accept a booking, schedule a car and send the car on a probably empty, and in any case, unbillable journey to the pick-up location, and wait whilst the passenger boards.
The fleet must be sized to meet peaks. Outside of peaks, much of the capacity of the fleet is wasted, so peak period travel "costs" the system more, which is passed on to peak travellers.
Peak per km rate
The default is $0.40
Off-peak flag fall
The default is $0.30
Off-peak per km rate
The default is $0.25
Other
Annual Fixed System cost
The default is $15,000,000
This cost is distinct from per-car and per-charger costs which are intended to fully cover their commissioning, operation and maintenance.
Rather, it is for costs which are largely fixed, regardless of fleet size, such as:
- liaison with customers, suppliers and government
- creation and maintenance of systems to facilitate car booking, billing and optimal operation of the fleet
Hard-coded model parameters
Peak periods
Used for peak/off-peak tariff calculations.
Car-sharing periods
During car-sharing periods, try to allocate passengers to an already "in-use" car, that is, a car already occupied by one or more passengers with at least one empty seat, either already travelling to the same destination as the new passenger, or "nearby", as long as the deviation to a new destination does not increase travel time by more than 20% or by more than 5 minutes for either the existing or prospective passengers.
Outside of car-sharing periods, an already "in-use" car will only be considered if there is no idle car nearby (that is, "in the same suburb") as the requesting passenger: if an idle car is available (as it almost always is outside of the car-sharing period), it will be used.
As a result, for most purposes, outside of car-sharing periods, a passenger almost always effectively books exclusive use of the entire car, whereas frequently during car-sharing periods, and particularly when travelling with the commuter "tide", a single seat, rather than the entire car, will be booked.Maximum range used
It is assumed that the battery is only charged to a level which will give it a range of 80% of the real-world maximum range.
This figure has been chosen to both honor the collective wisdom which asserts damage to current lithium ion batteries is minimised by not exceeding 80% charge, and to represent in the model battery degradation with age, particularly due to cycle frequency.
Range threshold to trigger recharging
When the remaining range falls to 25% of the the real-world maximum range (not the maximum range used) or 30km, the car will be routed to a recharger. It is possible that for small range simulations, some cars will embark on a trip longer than the remaining range. Yes, that is embarrassing, but it is something a real system would have to avoid and occasionally cope with by dispatching cars to pick-up passengers.
This figure has been chosen to both honor the collective wisdom that damage to current lithium ion batteries is minimised by not taking them under 20% charge, and the collective wisdom that cars shouldn't roll to a halt without power a long way from home.
Range threshold to trigger opportunistic recharging
If a car has been idle for at least 1 minute and has less than this range remaining, it will be routed to a recharger.
A high value of this setting may increase overheads by causing dead-running of the car to a charger. However, frequent "top ups" may be good for long battery life, and by charging in apparently idle times, may reduce wait times in peak periods.
Opportunistic recharging is throttled during the PM power use peak because charging can be safely deferred (anticipated demand is low) and the electricity grid is probably near capacity at that time.
Range threshold to trigger early morning recharging
If a car has been idle for at least 1 minute and has less than this range remaining, and the time is between 5am and 6am (ie, before the morning peak), it will be routed to a recharger.
The idea behind this setting is to attempt to top-up as many cars as possible before the morning peak, which you should see a charging burst starting at 5am. Depending on grid capacity and sources of power for EVs, this may or may not be appropriate.
Charging energy efficiency
The charging system is not 100% efficient. That is, when charging a battery, you will consume more energy from the grid than you can subsequently retrieve from the battery.
Figures of 85%-92% are commonly quoted, but the whole charging and system infrastructure will have power requirements of its own, so a figure of 85% should conservatively include these.
Max diversion overhead factor
When a car is already allocated and we're thinking of sharing it to a new destination, what is an acceptable increase in travel time for the allocated and possible new passenger caused by this "diversion"? This parameter specifies that an increase of up to 20% is ok.
Max diversion overhead minutes
When a car is already allocated and we're thinking of sharing it to a new destination, what is an acceptable increase in travel time for the allocated and possible new passenger caused by this "diversion"? This parameter specifies that an increase of up to 5 minutes is ok.
Off-peak travel time increase factor
Inter-suburb travel times are obtained from OpenStreetMap and GraphHopper. These times are rounded up to the next minute.
Peak travel time increase factor
Inter-suburb travel times are obtained from OpenStreetMap and GraphHopper. These times are increased by 15% for peak travel and rounded up to the next minute.
Pick-up and set-down times per passenger
When a car arrives at a pick-up or set-down point, it is assumed that each passenger will take 1 minute to embark or disembark. As well, if multiple passengers are being picked up from the same suburb, it is assumed that travelling from one pick-up point to the next pick up point will take an average of 1 minute. Ditto for set-downs.
It may be useful to model variable times. For example, a disabled passenger may take more than 1 minute to embark; 4 school kids arriving at their high school should take less than 7 minutes to disembark (4 x 1 minute set-down + 3 x 1 minute move-to-next-set-down-location).
Estimating non-weekday variable costs and revenues from weekday data
The number of non-weekday trips is estimated to be 70% of weekday trips. This is considerably below estimates of 85%-90% (see for example, the NSW Bureau of Transport Statistics 2011/12 Household Travel Survey).
However, for the purposes of this simulation, we are interested in the number of cars required and the fares that will be paid. The above-mentioned survey also indicates that work trips have a considerable lower average occupancy per car (1.10 people) compared to non-work trips (1.66), and non-work trips will be more likely on non-weekdays. Travel on non-weekdays will very rarely be shared by separate fare-paying passengers: almost all travel will be by fare payers paying for the entire car, rather than a seat, and so a family of four will travel for the same cost as one person. Hence, for revenue purposes, although the number of people travelling and the number of trips they take may be 85%-90% on non-workdays of the workday number, we conservatively estimate that the number of fares collected will be just 70% (and all will be at off-peak rates).
Unfortunately, this also implies that more than 70% of week-day car numbers will be required: basically, no car sharing is assumed, so "per km" non-weekday fleet costs (energy and maintenance) are inflated from the 70% level inversely proportional to the level of single occupancy trips made during a weekday.
For example, if 90% of weekday trips were single occupancy, then non-weekday "per km" costs are estimated as weekday "per km" costs times 0.7 and then divided by 0.9.
These calculations are probably slightly pessimistic (conservative) because the fleet is greatly underutilised during the non-weekdays and travel is less "peaky", so forced transfers between suburbs to meet demand and transfers to charging stations will be more than proportionally lower. On the other hand, there is some evidence that non-weekday trips may be shorter on average than weekday trips, as trips to work tend to be the longest journeys (at least as reported in the NSW Bureau of Transport Statistics 2011/12 Household Travel Survey).
Note, that you can mostly simulate a non-weekday outcome yourself, by specifying a per-hour traffic distribution and by making the peak and off-peak fares the same, setting vehicle capacity to 1 person (to eliminate any possibility of sharing and hence gathering multiple fares for a trip), and supplying the number of journeys (not passengers) you think are needed. You cannot, however, change the spatial distribution of journey (the source and destinations, which may be characteristically different enough on weekends to matter) without amending the contents of the TownsAndSuburbs.js file.
Workforce estimates
The following workforce estimates are based the default model with 34,000 cars each travelling 125,000km/yr and 1,200 chargers.
Car cleaning and charging staff (gross labour cost at casual rate of $40/hr including superannuation, or permanent rate equivalent)
- Per-charger visit, check and cleaning: 6 minutes, at an average 2.1 charges/working-day and 1.5 charges/other-day = 70 hrs/car/yr
- Weekly clean: 15 minutes = 13 hrs/car/yr
For 34,000 cars, the annual labour requirement is 2.8m hours, which at 32 (productive) hrs/week and 46 weeks-per-person/yr requires 1900 cleaning and charging staff.
1900 people x 35 hours paid/week x 46 weeks paid/year = 3.06m hours
Total cost: 3.06m hr/yr paid at $40/hr (inc super) = $122.4m/yr.
A permanent full-time car cleaner and charger paid for a 35 hour week will earn $1250/week plus superannuation of $150/week. A casual car cleaner and charger will earn $35.71/hr plus superannuation of $4.29/hr.
Administrative/management overhead adds 130 admin/management staff paid $110,000/yr (including superannuation)
Total cost: 130 people x $110,000/yr = $14.3m/yr.
Mechanics/electricians (gross labour cost of $100,000/yr including superannuation)
- Mechanics/electricians repairs/Maintenance labour estimate: 26 hrs/car/yr
- Charger maintenance estimate: 10 hrs/yr/charger
For 34,000 cars and 1200 chargers, annual labour requirement is 0.9m hours, at
32 (productive) hrs/week and 46 weeks-per-person/yr = 600 mechanics/electricians.
Total cost: 600 people x $100,000/yr = $60m/yr.
Administrative/management overhead and specialist fleet acquisition/commissioning/management staff adds
a further 90 admin/management staff paid $110,000/yr.
Total cost: 90 people x $110,000/yr = $9.9m/yr.
Other admin, technical specialist and management staff (average gross labour cost of $130k/yr)
- Corporate Management and support: 10 staff
- General Corporate (HR, finance, legal and marketing): 30 staff
- Technical specialists, scheduling and car systems: 20 staff
- IT support: 5 staff
Total: 65 staff, annual gross labour budget of $8.5m.
Other admin, technical specialist and management staff labour costs consumes 57% the model's default "Fixed Annual System Cost" budget on $15m. The remaining $7.5m is allocated to rent, equipment repairs and replacements, facilities, consumables and contracted services.
Workforce full-time-equivalent summary
- Cleaning and charging general staff: 1900
- Cleaning and charging management: 130
- Mechanics/electricians: 600
- Mechanics/electricians management: 90
- Corporate admin, technical specialist and management staff: 65
- Total: 2785 full-time-equivalent staff
Car consumables and parts summary for the default model
- 0.8 cents of the 6.0 cents/km default model maintenance costs are assumed to
be paid for tyres (ie, $400 for tyres every 50,000km)
- 0.9 cents of the 6.0 cents/km default model maintenance costs are assumed to
be paid for cleaning consumables and car parts (wiper blades, windscreen etc) related to per-km running costs (annual allowance of $1125/car/yr)
- $500 of the "administration and management" component of the $4000 annual fixed costs per care are assumed to allocated to consumables and parts needed
unpredictably but not covered by warranty, for example vandalism or accidental
damage, or wear-and-tear (annual allowance of $500/car/yr)
Annual income and expense summary for the default model
$M Note
Fare income $1282
Expenses $1178
Lease or capital & interest
$674
Cars
$663.3
Chargers
$10.1
Workforce
$215 FTE: 2785
Cleaning and charging operational
$122.4
FTE: 1970
Cleaning and charging management
$14.3
FTE: 130
Mechanics/electricians operational
$60.0
FTE: 600
Mechanics/electricians/fleet management
$9.9
FTE: 90
Admin, technical specialist and management staff
$8.5
FTE: 65
Parts
$90
Car tyres
$34.0
Per-km related parts and consumables
$38.3
Non per-km related parts and consumables
$17.0
Charger parts and consumables
$0.6
Insurances, rego, comms, workshop
$104
Electricity
$87
Other
$8
Charger rent
$0.6
Office rent, equipment repairs and replacements,
facilities, consumables and contracted services
$7.5
Operating Surplus $104
FTE: "full-time equivalent" number of staff
Sensitivity of operating surplus to various parameter settings
The following graphs show how the operating surplus is affected by changing various
financial assumptions, and how the operating surplus and percentage
of journeys with a waiting time of less than
1 minute are affected by varying the default assumption of number of journeys, keeping number of cars and chargers unchanged.
The "base" scenario is the Default 2022, with 34,000 cars, 1,200 charging stations and 1.1 million journeys per day, and only one parameter at a time is varied. Please note that the cost sensitivities were generated using a
per-km-cost of 5.5 cents per km, rather than the current default of 6.0 cents per km. At 5.5 cents per km, a typical surplus
of $127M is generated. At 6.0 cents per km, a typical surplus of $104M is generated.
For a given fleet, wait times (most particularly at peak periods) are very sensitive to
the number of journeys. Given the large financing fixed costs, surplus is also very sensitive to the number of journeys.
Electricity Price Update November 2025
From page 11 of AEMO's Quarterly Energy
Dynamics Q3 2025, October 2025:
In Q3 2025, wholesale electricity prices across the NEM averaged $87/MWh, down 27% from Q3 2024 and 38% from Q2
2025 (Figure 8). Lower price volatility and higher renewable output offset the impact of increased operational demand,
resulting in average prices of $109/MWh in July and $97/MWh in August. Seasonally lower demand and warmer sunnier
weather conditions pushed September prices further down to $53/MWh.
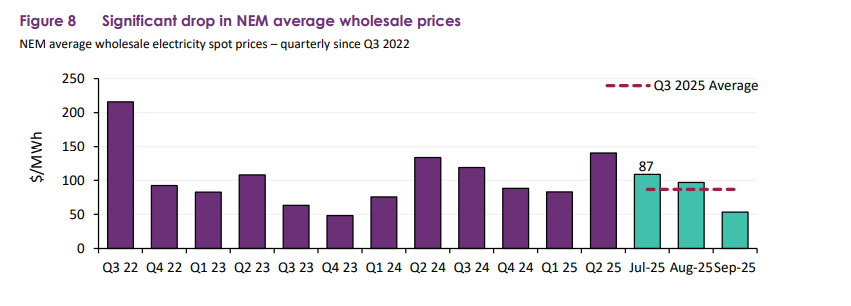
For the 3rd quarter 2025, average wholesale prices for NSW were slightly higher at $90/MWh. However, across the network, average prices were much lower outside peak usage hours and particularly lower between 9am and 4pm. From the same AEMO report, Figure 11 on page 15:
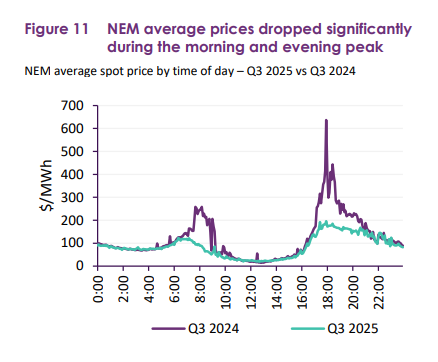
Peak pricing roughly coincide with transport peaks, during which most cars in the simulation are not being charged, and it is possible to move almost all car charging outside peaks. Hence, a complementary and easily implemented preference for charging outside these peaks would result in a wholesale electricity price of well under $90/MWh, that is, under 9 cents per kWh. Wholesale electricty prices were negative in the NSW region for 38% of the dispatch intervals between 9am and 5pm in the September 2025 quarter (compared to 33% for the same quarter 2024). For the 2nd quarter 2025, only 7% of dispatch intervals in NSW had negative pricing, but this was more than twice the number recorded for the same quarter in 2024.
Tranmission charges need to be added to this wholesale power cost.
From Transgrid's NSW and ACT Transmission Prices
1 July 2025 to 30 June 2026, the cost of transmission for, example, at Belconnen is a fixed $3,299 per day plus three costs based on the maximum power demanded during the month: a common service price of $2.28, a non-locational price of $0.43 and a Belconnen connection point specific locational price of $3.45, all measured in $/kW of maximum demand over the month.
Based on the default 2022 simulation, the maximum power demand from 216 chargers at Belconnen delivering a net 120 kW (but drawing a gross 141kW from the grid with the assumed 85% end-to-end efficiency) is 30494 kW. The total transmission costs (max kw plus daily costs) for a 30.5 day average month are hence $287k. The total energy demand from the Belconnen chargers for the average month from a typical simulation run (assuming 70% energy usage on weekend days compared to non-weekend days) is about 12,828,000 kW. Hence the typical network charge is about 2.24 cents per kWh.
Hence, even allowing a pessimistic average wholesale cost of 9 cents per kWh and the "rack" Transgrid transmission cost of 2.24 cents per kWh, an allowance of 12 cents per kWh seems realistic.
- 0.8 cents of the 6.0 cents/km default model maintenance costs are assumed to be paid for tyres (ie, $400 for tyres every 50,000km)
- 0.9 cents of the 6.0 cents/km default model maintenance costs are assumed to be paid for cleaning consumables and car parts (wiper blades, windscreen etc) related to per-km running costs (annual allowance of $1125/car/yr)
- $500 of the "administration and management" component of the $4000 annual fixed costs per care are assumed to allocated to consumables and parts needed unpredictably but not covered by warranty, for example vandalism or accidental damage, or wear-and-tear (annual allowance of $500/car/yr)
| $M | Note | |||||
|---|---|---|---|---|---|---|
| Fare income | $1282 | |||||
| Expenses | $1178 | |||||
| Lease or capital & interest | $674 | |||||
| Cars | $663.3 | |||||
| Chargers | $10.1 | |||||
| Workforce | $215 | FTE: 2785 | ||||
| Cleaning and charging operational | $122.4 | FTE: 1970 | ||||
| Cleaning and charging management | $14.3 | FTE: 130 | ||||
| Mechanics/electricians operational | $60.0 | FTE: 600 | ||||
| Mechanics/electricians/fleet management | $9.9 | FTE: 90 | ||||
| Admin, technical specialist and management staff | $8.5 | FTE: 65 | ||||
| Parts | $90 | |||||
| Car tyres | $34.0 | |||||
| Per-km related parts and consumables | $38.3 | |||||
| Non per-km related parts and consumables | $17.0 | |||||
| Charger parts and consumables | $0.6 | |||||
| Insurances, rego, comms, workshop | $104 | |||||
| Electricity | $87 | |||||
| Other | $8 | |||||
| Charger rent | $0.6 | |||||
| Office rent, equipment repairs and replacements, facilities, consumables and contracted services |
$7.5 | |||||
| Operating Surplus | $104 | |||||
FTE: "full-time equivalent" number of staff
The following graphs show how the operating surplus is affected by changing various financial assumptions, and how the operating surplus and percentage of journeys with a waiting time of less than 1 minute are affected by varying the default assumption of number of journeys, keeping number of cars and chargers unchanged.
The "base" scenario is the Default 2022, with 34,000 cars, 1,200 charging stations and 1.1 million journeys per day, and only one parameter at a time is varied. Please note that the cost sensitivities were generated using a per-km-cost of 5.5 cents per km, rather than the current default of 6.0 cents per km. At 5.5 cents per km, a typical surplus of $127M is generated. At 6.0 cents per km, a typical surplus of $104M is generated.
| For a given fleet, wait times (most particularly at peak periods) are very sensitive to the number of journeys. Given the large financing fixed costs, surplus is also very sensitive to the number of journeys. |
From page 11 of AEMO's Quarterly Energy Dynamics Q3 2025, October 2025:
In Q3 2025, wholesale electricity prices across the NEM averaged $87/MWh, down 27% from Q3 2024 and 38% from Q2 2025 (Figure 8). Lower price volatility and higher renewable output offset the impact of increased operational demand, resulting in average prices of $109/MWh in July and $97/MWh in August. Seasonally lower demand and warmer sunnier weather conditions pushed September prices further down to $53/MWh.
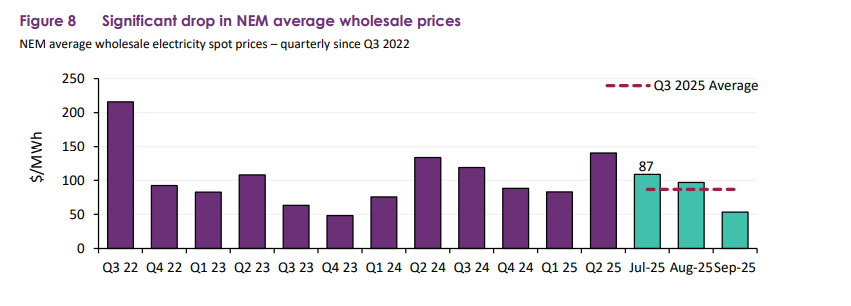
For the 3rd quarter 2025, average wholesale prices for NSW were slightly higher at $90/MWh. However, across the network, average prices were much lower outside peak usage hours and particularly lower between 9am and 4pm. From the same AEMO report, Figure 11 on page 15:

Peak pricing roughly coincide with transport peaks, during which most cars in the simulation are not being charged, and it is possible to move almost all car charging outside peaks. Hence, a complementary and easily implemented preference for charging outside these peaks would result in a wholesale electricity price of well under $90/MWh, that is, under 9 cents per kWh. Wholesale electricty prices were negative in the NSW region for 38% of the dispatch intervals between 9am and 5pm in the September 2025 quarter (compared to 33% for the same quarter 2024). For the 2nd quarter 2025, only 7% of dispatch intervals in NSW had negative pricing, but this was more than twice the number recorded for the same quarter in 2024.
Tranmission charges need to be added to this wholesale power cost. From Transgrid's NSW and ACT Transmission Prices 1 July 2025 to 30 June 2026, the cost of transmission for, example, at Belconnen is a fixed $3,299 per day plus three costs based on the maximum power demanded during the month: a common service price of $2.28, a non-locational price of $0.43 and a Belconnen connection point specific locational price of $3.45, all measured in $/kW of maximum demand over the month.
Based on the default 2022 simulation, the maximum power demand from 216 chargers at Belconnen delivering a net 120 kW (but drawing a gross 141kW from the grid with the assumed 85% end-to-end efficiency) is 30494 kW. The total transmission costs (max kw plus daily costs) for a 30.5 day average month are hence $287k. The total energy demand from the Belconnen chargers for the average month from a typical simulation run (assuming 70% energy usage on weekend days compared to non-weekend days) is about 12,828,000 kW. Hence the typical network charge is about 2.24 cents per kWh.
Hence, even allowing a pessimistic average wholesale cost of 9 cents per kWh and the "rack" Transgrid transmission cost of 2.24 cents per kWh, an allowance of 12 cents per kWh seems realistic.
